Difference between revisions of "The Swing-in"
Wonneproppen (talk | contribs) |
Wonneproppen (talk | contribs) |
||
| (10 intermediate revisions by 8 users not shown) | |||
| Line 2: | Line 2: | ||
|- | |- | ||
| | | | ||
| − | + | A loudspeaker tries to reproduce transients by transient oscillation. This transient response occurs according to its transfer function, provided there are no nonlinearities, e.g. [[resonances]]. Chassis behave completely differently when reproducing a first half-wave than they do when transient. This is due to the inability of electroacoustic transducers to fully reproduce the first half-wave of an oscillation (e.g. sine, sine burst, or even music signal). Strictly speaking, a chassis can only reproduce the first half-wave with the correct frequency at exactly one single frequency! The transfer function describes the transient response and the difference between the first and the following half-waves, the quasi-swinged state. It is characterized by a high pass in the woofer and a low pass in the tweeter, both of which determine the limits of the bandwidth of the loudspeaker. And both show an opposite behavior in the transient distortion of the signals. This means that during transient response the low frequencies (= high pass) and the high frequencies (= low pass) are cut off and the speaker has a lower bandwidth than the frequency response shows. In the case of complex resonance phenomena, however, a simple transfer function fails completely. In principle, a loudspeaker can only transpose correctly over the entire (or its average) bandwidth, if it shows a rectangular or rectangle-like behaviour. Only then would the first half-waves within this bandwidth be correct in amplitude and phase.<br /> | |
| − | + | The term ''transients'' is used for sound events. Transients are initial noises with a broad frequency spectrum, whose signal forms by nature do not correspond to any given definition (they are not determined / calculated in any way). The transient of the technical system loudspeaker is not called transient.<br /> | |
| − | + | The time resp. number of oscillations a loudspeaker needs until it can follow the input signal is called ''transient''. The time or number of oscillations that a loudspeaker follows the input signal is called ''steady state''. <br /> | |
| − | '' | + | ''Transient distortion is heard in the transient, not in the continuous tone!''<br /> |
| − | + | The sine wave as a short signal (≈ 0.5 or 1 period) is actually aurally unrecognizable as such during distorted playback, or it is a completely different, artificial sound. This can be experienced immediately when listening during the measurement. As a continuous tone, on the other hand, it can be heard, because then these transient distortions no longer exist. This behaviour is also clearly audible with noise or also very clearly with applause. If you switch between different loudspeakers you will hear that the applause varies extremely, because each loudspeaker has a different distortion profile. The fact that steeply filtered speakers sometimes sound lame and lifeless is evidence that the transients are distorted. The impulses lose volume and contour and change the sound into artificiality.<br /> | |
| | | | ||
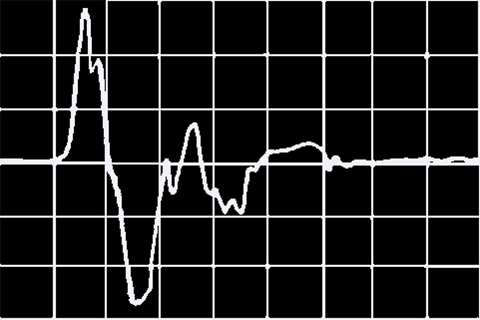
| − | [[ | + | [[File:Shot.png]]<br /> |
| − | '' | + | ''Sound structure of a pistol shot''<br /> |
| − | '' | + | ''Source: Manger Company'' |
|} | |} | ||
| − | + | For the most part, it is assumed that the loudspeaker will transient on jump excitation such that it exhibits the characteristics (frequency response, etc.) that it exhibits when transient. This is not the case! For the steady state characteristic (amplitude), the ''complete'' oscillation process is necessary until the steady state is reached. If however already after reaching the ''first'' maximum voltage value of the jump no voltage change in the sense of alternating voltage is present, the drive of the chassis ends with it. In nature there are such excitations, for example:<br /> | |
| − | * | + | *explosions, gun shots, etc. |
| − | * | + | *percussion instruments with vibration damping (hardly any reverberation) |
| − | * | + | *hand clapping / applause |
| − | * | + | *and many more. |
| − | + | The chassis then only resonates over or after. It does this in the direction of its resonance frequency, but without emitting any significant sound pressure, especially none that is added a few milliseconds later. Therefore, the response of the driver is completed much sooner. If you excite a loudspeaker with a jumpy waveform without any further oscillations, it will not reach the steady state either and all the models that assume this do not apply. The "backward oscillation" with the zero crossing at completely accelerated mass is missing and thus the complete oscillation of the spring-mass system. Only when this process has been passed, one can speak of a steady state. Some loudspeakers reach this (depending on the quality) even later. | |
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
|- | |- | ||
| | | | ||
| − | == | + | == Tweeter == |
| − | + | The dynamic music signal is all about speed. The rising edges and times of the impulses depend on the ability of the tweeter to settle extremely quickly. In the case of the tweeter, at the upper transmission end, the resonant frequency of the diaphragm is particularly crucial. But if a tweeter transmits very high frequencies in the frequency response diagram, this does not mean that it is fast. With many tweeters the frequency response is only up to 20 kHz because the low pass and the diaphragm resonance have been tuned in such a way that the result is an almost linear response in the ''steady state''. This can be seen by a steep drop above the resonance frequency, i.e. at the end of the frequency range visible in the frequency response. A high treble level, caused by the diaphragm resonance, has to settle down first, and that takes two to three half waves! However, the signal / time response usually looks bad from 5 to 10 kHz.<br /> | |
| − | + | The transients (1st half-wave) do not occur at the excitation frequency due to the low-pass behaviour, they regularly contain lower frequencies and the amplitude is significantly below the value in the transient state. They last longer than the input signal and thus cause a lagging phase. Sonically, this means that the high frequency pulses are too quiet and too low in pitch. However, the steady-state frequency response makes us believe something completely different! If the system's low pass acts only at very high frequencies, as for example with the [[Myro Amur D]] with diamond tweeter, then the transient response (the starting edge of the step response) is so fast that you almost get a square wave. A lower low pass causes a delay of the energy and thus a time delayed adding up and thus the typical ramp of a typical "time correct" loudspeaker. Of course, you can still see the high pass in the slope of the graph. In between the speaker is very broadband phase linear.<br /> | |
| − | ''' | + | '''What quality must a transmission line have if a person consciously perceives 16 kHz without restriction?"''<br /> |
| − | + | The effect on waveform and timing by filters or the natural low-pass of a tweeter extends several octaves lower. In order to be able to reproduce 16 kHz without timing shift and without corresponding signal deformation, all quality-reducing phenomena must only take effect above 16 kHz. In measurement technology, one keeps a "distance" of at least 2 - 3 octaves to the measurement object in order to keep the influence of the measurement equipment itself out of the result. A tweeter or a signal source must therefore also have a "distance" of 2 - 3 octaves to the human hearing range. Even if the audible range was only defined up to 16 kHz, a distance of only 2 octaves would already result in 64 kHz. And that's close! So high-resolution source material is a must. A tweeter that reproduces 16 kHz without errors is also a must. But if the tweeter, as usual, already has its diaphragm resonance at 20 - 30 kHz and the influence of the low pass already starts in the upper mids, one will hardly be able to detect quality differences of the signal sources. | |
| − | + | Remarkable are the specifications of the upper cut-off frequency (-3 dB) by some manufacturers. For example, an upper cut-off frequency of 100 kHz is declared for the Accuton BD20 (20 mm diamond cone). In fact, however, according to measurements by the driver manufacturer, the -3 dB point is at ≈ 44 kHz, but this is without a main diaphragm resonance overlapping. | |
| − | + | This is at ≈ 60 kHz (about -10 dB point / depending on the mic). The manufacturer has therefore "glossed over" the 100 kHz by more than an octave! <br /> | |
| | | | ||
| − | [[ | + | [[File:Lautsprecher-purus-11-by-michael-weidlich.jpg]]<br /> |
''[[Myro Purus 1.1]]'' | ''[[Myro Purus 1.1]]'' | ||
|} | |} | ||
| Line 41: | Line 41: | ||
|- | |- | ||
| | | | ||
| − | [[ | + | [[File:Subtronik.jpg]]<br /> |
''[[Myro Subtronik]]'' | ''[[Myro Subtronik]]'' | ||
| | | | ||
| − | == | + | == woofer == |
| − | + | In the low bass range, we are at the physical limits of the transducers, which are limited in their geometric dimensions, and the enclosures necessary to avoid acoustic short circuits. To produce deep bass is a trivial task for a loudspeaker designer. But finding a customer for such a large speaker is a very difficult task. There are ''always'' restrictions on the part of the user concerning the size of a loudspeaker and also concerning the price. The "ideal" of the small, slim, pretty floorstanding speaker has the consequence that if one wants to meet this not insignificant demand, with these physical limitations one can in principle build a loudspeaker that is correct in time (simultaneity of transient response and linear phase), but these speakers lack the ability to produce bass dynamics that do justice to the dynamics of the mid-high range (cf. first half wave). But forcing woofers with large amplifier power to reproduce low bass against the high compression of small enclosure volumes not only deforms their diaphragm, but also heats their voice coils. Hot voice coils become even more highly resistive with each burst of heat. That's built-in compression, since amplifiers deliver less power to high-impedance loads. You also have to think of it in terms of rhythm. So keeping the frequency response in the bass at a high level is not the problem, but the transient, the impulse dynamics is.<br /> | |
| − | + | The reproduction of 20 Hz is not enough either. To generate the first half wave with correct amplitude and frequency, and thus also with linear group delay and phase, a huge diaphragm area is needed for physical reasons. A 15 inch speaker is far from sufficient for this. The sound wave propagates at the speed of sound while the woofer diaphragm is moving. A woofer, with its small diaphragm in relation to the wavelength, has to generate pressure with a sound wave travelling at a speed of approx. 345 m/s. This requires an extremely wide excursion of the diaphragm. This requires an extremely wide excursion to faithfully reproduce the first half-wave, such as the beat of a bass drum. Even the excursion of long excursion drivers is completely insufficient for this. But even half a wavelength takes an eternity in relation to the speed of sound. Low frequencies are slow oscillations and the wave quickly leaves the area of the membrane surface at low frequencies. This results in a very low radiation resistance and a low efficiency. <br /> | |
| − | + | The bass response is elementally determined by the radiation resistance and the resonance case of the vibrating system. Both aspects interact and involve time constants, i.e. they have a time response. Frequency response measurements only show the sound amplitude values of the resonance case that has occurred. Due to the time constant, however, these are only reached with a delay. Before that, during transient response, a loudspeaker behaves according to the radiation resistance curve, resulting from membrane area and membrane velocity (frequency). Added to this are the non-linearities of the drive.<br /> | |
| − | + | The amplitude frequency response at the lower end of the transmission is characterized by the temporal transition of the high pass caused by the radiation resistance to the high pass caused by radiation resistance and resonance. The high-pass function of a loudspeaker is essentially a superposition of three functions: | |
| − | # | + | # the function of radiation resistance |
| − | + | the function of the mechanical oscillating system (resonance frequency) | |
| − | # | + | # the electrical function (BxL + voice coil inductance and ohmic resistance). |
| − | + | The spring-mass system plays a crucial role in the formation of the first half-wave. It is tensioned (energy storage) and acts in the opposite direction to the drive direction. At the point where the drive energy and counterforce of the spring-mass system are equal, only the energy of the moving mass causes a brief further forward movement. This (system resonance), together with the radiation resistance, produces the high-pass characteristic.<br /> | |
| − | + | All functions have a time constant. The transient response of a loudspeaker is subject to several complex time constants. So if you have a certain demand on the transmission behaviour in the low frequency range, you have to define exactly what you mean by this. To reproduce a bass drum correctly requires a gigantic bass speaker with corresponding cabinet conditions. In the case of resonance, the required frequency range can be generated by the usual formats, even mini cabinets could be made to do this, but in the transient, the most striking and loudest moment of a bass drum, small speakers have no chance!<br /> | |
| − | + | Due to the high pass behaviour woofers swing in with a too weak first half wave. The first half wave also has a frequency spectrum whose lowest equivalent frequency is higher than the excitation signal and it has an early zero crossing, which also explains the leading phase in the phase frequency response. When measuring with a sine burst you can see that the first half wave is much smaller and shorter than the following waves. This means bass speakers get progressively weaker towards low notes at the beginning of a sound event and only settle to the level we can see in the amplitude frequency response diagram at the second half-wave. The usual frequency response measurement deceives us with sound pressure that is not yet present in the transient.<br /> | |
| + | |} | ||
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
| Line 61: | Line 62: | ||
| | | | ||
<gallery> | <gallery> | ||
| − | + | File:P m frequ nah.jpg|Frequency response<br /> | |
<br /> | <br /> | ||
| Line 67: | Line 68: | ||
| | | | ||
<gallery> | <gallery> | ||
| − | P m 3d front.jpg|''3-D Dynamic Measurement (0 | + | P m 3d front.jpg|''3-D Dynamic Measurement (0.5 period sine / from 100 Hz)'' |
</gallery> | </gallery> | ||
| | | | ||
| − | '' | + | ''Example:''<br /> |
| − | '' | + | ''In the steady state, the bass of this speaker drops at about 75 Hz (frequency response measurement). In the steady state with a positive excitation / half wave, however, this is already the case from 300 Hz (or even higher). In the corresponding 3-D half-wave measurement, the resonance of the oscillating system has not yet settled and the corresponding sound pressure component is missing. We see here above all the influence of the radiation resistance.'' |
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | With all cabinet tunings that make use of a resonant system (e.g. bass reflex, transmission line, etc.) to amplify the bass sound pressure, this illusion is even much greater! A resonant system needs several half-waves to resonate and add additional sound pressure. The behaviour corresponds to the transfer function. However, the first half-waves are not stronger than in a closed cabinet, because here the resonance behaviour is not yet effective. It shows that there is a serious difference between the transient and the steady state. <br /> | |
| − | |||
| − | |||
| − | |||
| + | '''The Bandpass'''<br /> | ||
| + | Basically, a bandpass oscillates extremely slowly. The amplitude shown in the frequency response is only reached after several half-waves (at the earliest from the third half-wave, although this is continuously increasing). Even if you would place a bandpass loudspeaker in such a way that the generated sound wave would start at the same time as the mid-high segment, in many cases you would have problems with an antiphase polarity. Helpful for the metrological representation of the transient response are, besides the not so easy to interpret step response, the front view of waterfall diagrams or even more descriptive, oscilloscope measurements with sinus bursts. <br /> | ||
| + | Let's look at the transient response of instruments and sounds: In natural sound events, the first half-waves are usually the loudest. The following half waves become quieter more or less quickly. Thus we have an unnatural, opposite behaviour with loudspeakers. This is even more unnatural with cabinet tuning with additional resonance system, because the ratio of first to following half waves becomes even more opposite. The better the overall phase response of a loudspeaker becomes in the mid and upper range (also in the transient), the more the bad behaviour towards low tones becomes noticeable.<br /> | ||
| + | Even in a closed cabinet the drivers have a delayed transient response. Regardless of the enclosure / tuning principle, the first half-waves have a high-pass characteristic that is practically always the same, which in principle corresponds to the effective part of the radiation impedance. | ||
| − | ''' | + | '''The bass reflex system''''<br /> |
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
|- | |- | ||
| | | | ||
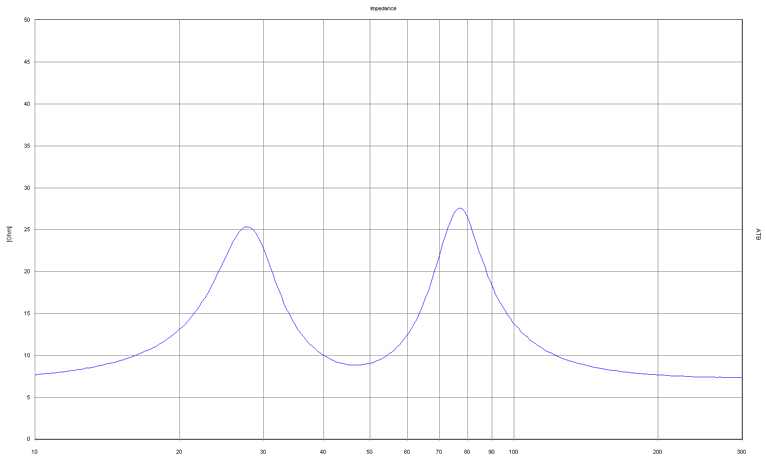
| − | [[ | + | [[File:BR-Imp.10-300 Hz.jpg]] |
| | | | ||
| − | + | In principle, the same applies to the bass reflex principle as to the bandpass. Based on the mode of operation it can be shown that such a resonant system needs a certain time to settle down: | |
| − | + | A bass reflex system adds additional energy only after two to three half waves. The first half-waves of natural instruments (or other natural sound events), which are particularly loud, therefore benefit little or not at all from a bass reflex system. During impulse reproduction, the sound energy of the resonance system is not yet available!<br /> | |
| + | Closing the bass reflex tube changes practically nothing in the impulse reproduction. Listening tests show time and again that closed systems produce a more natural, truer sound. The prerequisite for this is that the woofer is able to deliver sufficient energy and that its tuning in the overall system is seamless. Loudspeakers with very small woofers, on the other hand, usually cannot manage without bass reflex. Otherwise the bass is simply not there. The delayed "roll-off" of the bass reflex sound is spectacular but always reminds you that you are listening to a loudspeaker, even with a cleanly tuned bass reflex. | ||
| − | + | The graph on the left shows the impedance curve of a bass reflex tuning. | |
| − | + | The two typical peaks are clearly visible, in between is the tuning frequency of the system. | |
|- | |- | ||
| | | | ||
| − | + | The time curve (cosine burst) / waterfall diagram front view<br /> | |
| − | [[ | + | [[File:BR-Imp.-Zeit cos.10-300 Hz Front.jpg]] |
| | | | ||
| − | + | The time course / rear view<br /> | |
| − | [[ | + | [[File:BR-Imp.-Zeit cos.10-300 Hz Back.jpg]] |
|} | |} | ||
| + | |||
| + | === Transient response of a multi-way loudspeaker === | ||
| + | From the frequency from which a chassis reaches the matching to the air, the chassis can already reproduce the first half wave with full amplitude and correct zero spacing (corresponding to the input frequency). Therefore, in this range (up to the low pass) a linear phase reproduction can be realized. And with multiple paths the range can be extended, depending on the high pass of the woofer and the low pass of the tweeter. The loudspeaker has a linear-phase range and a minimum-phase range in the low-pass and high-pass regions. Therefore, rectangles can be reproduced in certain transmission ranges. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | | ||
| + | [[File:Step N-.jpg]] | ||
| + | | | ||
| + | On the left is an actual example of a digital speaker from a very reputable company. The humps / waves starting at 20.5 ms are due to initial reflections.<br> | ||
| + | Relevant for the above consideration is the range from ≈ 18.5 to ≈ 20.5 ms. Even if the sound components of the negative preoscillators were properly added in time and amplitude, the loudspeaker would still plateau until the pressure could no longer be sustained due to the high-pass. The loudspeaker is optimized for a linear-phase transmission range and achieves this goal over a span of about 1 ms. | ||
| + | |- | ||
| + | [[File:Sinus N 1.000 Hz.jpg]] | ||
| + | | | ||
| + | The reproduction of a 1,000 Hz sine wave (1 period) looks like this.<br> | ||
| + | Apart from the negative pre-oscillation and the too early end of the second half-wave (the system is overdamped), the loudspeaker forms two half-waves of equal amplitude and duration. | ||
| + | This is typical for a correct match to the air. | ||
| + | |- | ||
| + | [[File:Sinus N 100 Hz.jpg]] | ||
| + | | | ||
| + | At 100 Hz, however, this behavior is long gone. The first half wave does not have the full amplitude and not the full duration. The loudspeaker behaves again like a typical minimum phase system with a correspondingly decreasing step response. | ||
| + | |||
| + | As an aside, there are again very strange digital artifacts to be seen: There are straight sections in the half waves. Whether these are errors in the calculation or fundamental problems in the attempt of a linear group delay is still unclear. | ||
| + | |} | ||
| + | |||
| + | === What can be technically corrected? === | ||
| + | |||
| + | '''Digitally...'''<br /> <br /> | ||
| + | the group delay can be equalized, but the problem of the missing amplitude always remains in the transient - in the period, where the radiation resistance curve sets the basic conditions, before the resonance case occurs. A group delay correction alone does not result in a correct signal conversion! This is because the signal contains a sequence of pressure fluctuations (pressure values). The group delay error is caused by the imperfect transient response due to the laws of physics. The first half wave is not fully formed by bass speakers, i.e. the first zero crossing occurs well before 180 degrees. The bass is leading! Filters delay with increasing order increasingly in the range of the low pass. This contains a clear amplitude error. However, it is physically impossible to achieve the correct time-amplitude relationships in the limit ranges of the transmission system. If one wanted to correct the pressure-time error of the transient, one would have to push so much energy into the systems transient that the drivers would be destroyed or the bass would make an extreme excursion across the room. And even that would not help. | ||
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
|- | |- | ||
| | | | ||
| − | + | [[File:Digital-LS sinus 40Hz.jpg]] | |
| + | | | ||
| + | Another problem is shown by the following measurement of a woofer that oscillates at 40 Hz (sine). A chassis control first requires the acquisition of a certain amount of data in order to be able to apply mathematics at all. The digital control starts accordingly delayed. After a certain time, it recognizes the deviation of the actual from the target, sets in and readjusts. However, the process takes place visibly abruptly and therefore contains (spectral analysis) significantly higher frequencies. <br /> | ||
| + | This jump sounds like a touch noise superimposed on the bass signal, which did not exist at all in the original instrument. Without regulation, however, such an error is impossible. | ||
| + | In the steady state the speaker follows the signal as if on rails (a driver with excellent drive does this even without control), but in the steady state it produces a violent jump. | ||
| − | + | What remains is the practical maximum size of the diaphragm area and the required construction, to be determined by each individual. For these individual requirements loudspeakers have to be developed in corresponding, always limited sizes. And these should convert as correctly as possible within the physically possible transmission range.<br /> | |
| − | + | |} | |
| − | |||
| + | {| class="wikitable" border="1" | ||
| + | |- | ||
| + | | | ||
| + | '''Control by analog sensor'''<br /> | ||
| + | At the lower transmission end of a chassis, where at least one stiff diaphragm vibrates as a unit, deviations from the target can be detected inductively. This is basically the chance for a control with inductive detector. But exactly in this transmission range there is a problem that can only be controlled to a very limited extent, namely the reactive component that increases at low frequencies due to the radiation resistance curve. This is particularly evident when measuring with sinusoidal bursts. In the steady state, the bursts decrease in amplitude with decreasing frequency. This also corresponds to the frequency response measurements. With decreasing frequency, the transients not only show a decreasing amplitude, but also premature zero crossings, the leading phase. Equivalent to the frequency consideration they contain as lowest possible wave a frequency which lies much higher than the excitation frequency. If one wanted to counter-regulate, one would massively overload the chassis (because almost only reactive component). This is a physically senseless undertaking. <br /> | ||
| − | + | Similarly problematic is the correction of room induced cancellations. Regulation brings advantages at the lower transmission end, especially in the steady state. However, the steady state is completely subject to room resonance problems in the bass, with all the effects and limitations of attempting correction. Directly diaphragm controlled basses ignore changes in the radiation resistance of the room and therefore excite modes more than unregulated speakers or even microphonically controlled ones. This is because the controlled loudspeaker doesn't act as a "soft bass trap" but as a "hard wall" with regard to any external excitation of the diaphragm that doesn't succeed. However, the difference to unregulated loudspeakers is only slight, as there is an extreme acoustic mismatch.<br /> | |
| − | + | With cone drivers there is hardly any effect, but only with flat radiators, i.e. systems without internal negative feedback in the cabinet (extremely low generated microphone voltage) and very low mass and large surface area (and little excursion), thus very low resonance quality and (relatively) high acoustic matching. | |
| − | + | In the bass you would have to correct the room, otherwise it makes no sense. But this is only possible to a very limited extent, and if so - for which space in the room? In addition, room resonances easily cause 10 dB amplitude fluctuations. That's mighty compared to the effect of a control. So the detector must be at the listening position!<br /> | |
| − | + | In the middle and especially in the upper transmission range of a chassis the manifold resonance phenomena (membrane resonances, [[resonances]] of or with the spider and with the edge suspension etc.) can no longer be detected inductively. The resonances no longer have a clear effect on the drive system with their kinetic energy. | |
| − | + | A control is therefore no longer possible in a meaningful way in the largest part of the transmission range. A control system works better here. | |
| | | | ||
| − | [[ | + | [[File:Amur.jpg]]<br /> |
| − | [[Myro Amur C]] | + | ''[[Myro Amur C]] Caramel'' |
|} | |} | ||
Latest revision as of 15:17, 20 January 2019
|
A loudspeaker tries to reproduce transients by transient oscillation. This transient response occurs according to its transfer function, provided there are no nonlinearities, e.g. resonances. Chassis behave completely differently when reproducing a first half-wave than they do when transient. This is due to the inability of electroacoustic transducers to fully reproduce the first half-wave of an oscillation (e.g. sine, sine burst, or even music signal). Strictly speaking, a chassis can only reproduce the first half-wave with the correct frequency at exactly one single frequency! The transfer function describes the transient response and the difference between the first and the following half-waves, the quasi-swinged state. It is characterized by a high pass in the woofer and a low pass in the tweeter, both of which determine the limits of the bandwidth of the loudspeaker. And both show an opposite behavior in the transient distortion of the signals. This means that during transient response the low frequencies (= high pass) and the high frequencies (= low pass) are cut off and the speaker has a lower bandwidth than the frequency response shows. In the case of complex resonance phenomena, however, a simple transfer function fails completely. In principle, a loudspeaker can only transpose correctly over the entire (or its average) bandwidth, if it shows a rectangular or rectangle-like behaviour. Only then would the first half-waves within this bandwidth be correct in amplitude and phase. |
For the most part, it is assumed that the loudspeaker will transient on jump excitation such that it exhibits the characteristics (frequency response, etc.) that it exhibits when transient. This is not the case! For the steady state characteristic (amplitude), the complete oscillation process is necessary until the steady state is reached. If however already after reaching the first maximum voltage value of the jump no voltage change in the sense of alternating voltage is present, the drive of the chassis ends with it. In nature there are such excitations, for example:
- explosions, gun shots, etc.
- percussion instruments with vibration damping (hardly any reverberation)
- hand clapping / applause
- and many more.
The chassis then only resonates over or after. It does this in the direction of its resonance frequency, but without emitting any significant sound pressure, especially none that is added a few milliseconds later. Therefore, the response of the driver is completed much sooner. If you excite a loudspeaker with a jumpy waveform without any further oscillations, it will not reach the steady state either and all the models that assume this do not apply. The "backward oscillation" with the zero crossing at completely accelerated mass is missing and thus the complete oscillation of the spring-mass system. Only when this process has been passed, one can speak of a steady state. Some loudspeakers reach this (depending on the quality) even later.
ContentsTweeterThe dynamic music signal is all about speed. The rising edges and times of the impulses depend on the ability of the tweeter to settle extremely quickly. In the case of the tweeter, at the upper transmission end, the resonant frequency of the diaphragm is particularly crucial. But if a tweeter transmits very high frequencies in the frequency response diagram, this does not mean that it is fast. With many tweeters the frequency response is only up to 20 kHz because the low pass and the diaphragm resonance have been tuned in such a way that the result is an almost linear response in the steady state. This can be seen by a steep drop above the resonance frequency, i.e. at the end of the frequency range visible in the frequency response. A high treble level, caused by the diaphragm resonance, has to settle down first, and that takes two to three half waves! However, the signal / time response usually looks bad from 5 to 10 kHz. 'What quality must a transmission line have if a person consciously perceives 16 kHz without restriction?" Remarkable are the specifications of the upper cut-off frequency (-3 dB) by some manufacturers. For example, an upper cut-off frequency of 100 kHz is declared for the Accuton BD20 (20 mm diamond cone). In fact, however, according to measurements by the driver manufacturer, the -3 dB point is at ≈ 44 kHz, but this is without a main diaphragm resonance overlapping.
This is at ≈ 60 kHz (about -10 dB point / depending on the mic). The manufacturer has therefore "glossed over" the 100 kHz by more than an octave! |
wooferIn the low bass range, we are at the physical limits of the transducers, which are limited in their geometric dimensions, and the enclosures necessary to avoid acoustic short circuits. To produce deep bass is a trivial task for a loudspeaker designer. But finding a customer for such a large speaker is a very difficult task. There are always restrictions on the part of the user concerning the size of a loudspeaker and also concerning the price. The "ideal" of the small, slim, pretty floorstanding speaker has the consequence that if one wants to meet this not insignificant demand, with these physical limitations one can in principle build a loudspeaker that is correct in time (simultaneity of transient response and linear phase), but these speakers lack the ability to produce bass dynamics that do justice to the dynamics of the mid-high range (cf. first half wave). But forcing woofers with large amplifier power to reproduce low bass against the high compression of small enclosure volumes not only deforms their diaphragm, but also heats their voice coils. Hot voice coils become even more highly resistive with each burst of heat. That's built-in compression, since amplifiers deliver less power to high-impedance loads. You also have to think of it in terms of rhythm. So keeping the frequency response in the bass at a high level is not the problem, but the transient, the impulse dynamics is.
the function of the mechanical oscillating system (resonance frequency)
The spring-mass system plays a crucial role in the formation of the first half-wave. It is tensioned (energy storage) and acts in the opposite direction to the drive direction. At the point where the drive energy and counterforce of the spring-mass system are equal, only the energy of the moving mass causes a brief further forward movement. This (system resonance), together with the radiation resistance, produces the high-pass characteristic. |
|
|
|
Example: |
With all cabinet tunings that make use of a resonant system (e.g. bass reflex, transmission line, etc.) to amplify the bass sound pressure, this illusion is even much greater! A resonant system needs several half-waves to resonate and add additional sound pressure. The behaviour corresponds to the transfer function. However, the first half-waves are not stronger than in a closed cabinet, because here the resonance behaviour is not yet effective. It shows that there is a serious difference between the transient and the steady state.
The Bandpass
Basically, a bandpass oscillates extremely slowly. The amplitude shown in the frequency response is only reached after several half-waves (at the earliest from the third half-wave, although this is continuously increasing). Even if you would place a bandpass loudspeaker in such a way that the generated sound wave would start at the same time as the mid-high segment, in many cases you would have problems with an antiphase polarity. Helpful for the metrological representation of the transient response are, besides the not so easy to interpret step response, the front view of waterfall diagrams or even more descriptive, oscilloscope measurements with sinus bursts.
Let's look at the transient response of instruments and sounds: In natural sound events, the first half-waves are usually the loudest. The following half waves become quieter more or less quickly. Thus we have an unnatural, opposite behaviour with loudspeakers. This is even more unnatural with cabinet tuning with additional resonance system, because the ratio of first to following half waves becomes even more opposite. The better the overall phase response of a loudspeaker becomes in the mid and upper range (also in the transient), the more the bad behaviour towards low tones becomes noticeable.
Even in a closed cabinet the drivers have a delayed transient response. Regardless of the enclosure / tuning principle, the first half-waves have a high-pass characteristic that is practically always the same, which in principle corresponds to the effective part of the radiation impedance.
The bass reflex system'
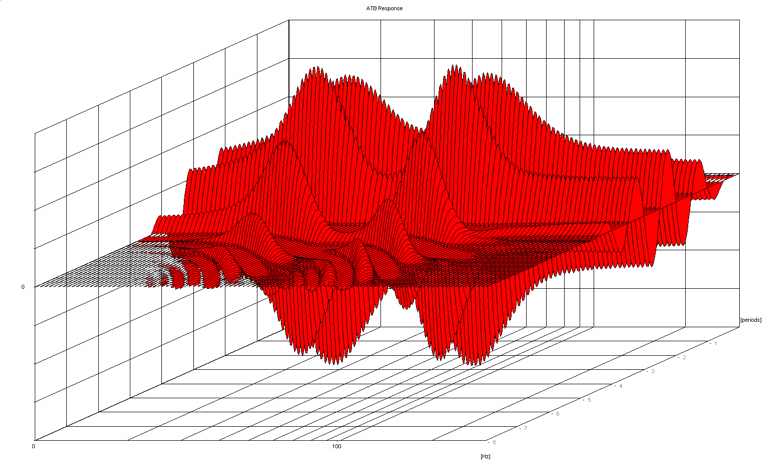
Transient response of a multi-way loudspeaker
From the frequency from which a chassis reaches the matching to the air, the chassis can already reproduce the first half wave with full amplitude and correct zero spacing (corresponding to the input frequency). Therefore, in this range (up to the low pass) a linear phase reproduction can be realized. And with multiple paths the range can be extended, depending on the high pass of the woofer and the low pass of the tweeter. The loudspeaker has a linear-phase range and a minimum-phase range in the low-pass and high-pass regions. Therefore, rectangles can be reproduced in certain transmission ranges.
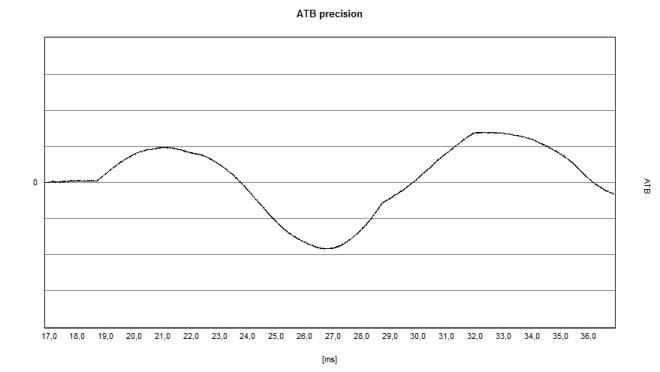
|
On the left is an actual example of a digital speaker from a very reputable company. The humps / waves starting at 20.5 ms are due to initial reflections. | |
|
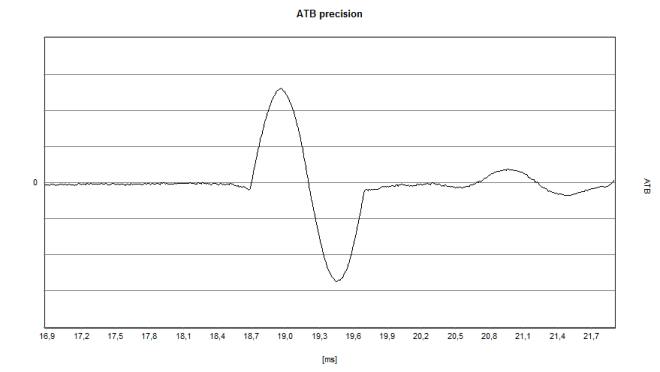
The reproduction of a 1,000 Hz sine wave (1 period) looks like this. | |
|
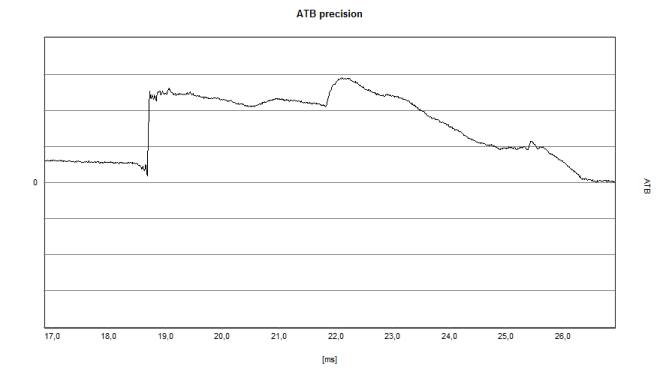
At 100 Hz, however, this behavior is long gone. The first half wave does not have the full amplitude and not the full duration. The loudspeaker behaves again like a typical minimum phase system with a correspondingly decreasing step response. As an aside, there are again very strange digital artifacts to be seen: There are straight sections in the half waves. Whether these are errors in the calculation or fundamental problems in the attempt of a linear group delay is still unclear. |
What can be technically corrected?
Digitally...
the group delay can be equalized, but the problem of the missing amplitude always remains in the transient - in the period, where the radiation resistance curve sets the basic conditions, before the resonance case occurs. A group delay correction alone does not result in a correct signal conversion! This is because the signal contains a sequence of pressure fluctuations (pressure values). The group delay error is caused by the imperfect transient response due to the laws of physics. The first half wave is not fully formed by bass speakers, i.e. the first zero crossing occurs well before 180 degrees. The bass is leading! Filters delay with increasing order increasingly in the range of the low pass. This contains a clear amplitude error. However, it is physically impossible to achieve the correct time-amplitude relationships in the limit ranges of the transmission system. If one wanted to correct the pressure-time error of the transient, one would have to push so much energy into the systems transient that the drivers would be destroyed or the bass would make an extreme excursion across the room. And even that would not help.
|
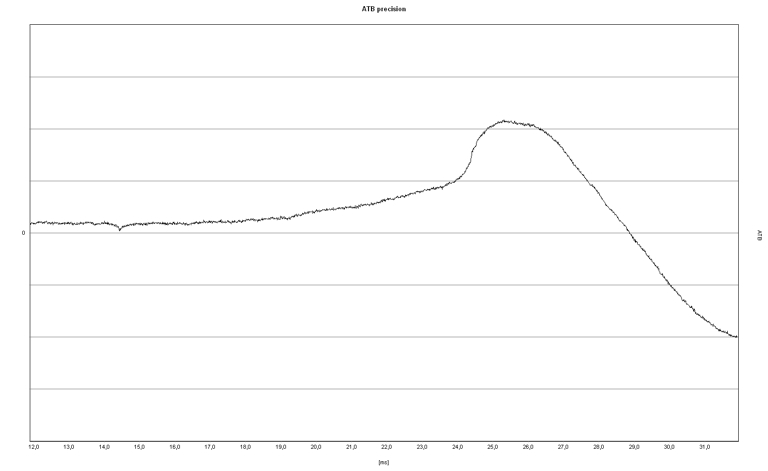
Another problem is shown by the following measurement of a woofer that oscillates at 40 Hz (sine). A chassis control first requires the acquisition of a certain amount of data in order to be able to apply mathematics at all. The digital control starts accordingly delayed. After a certain time, it recognizes the deviation of the actual from the target, sets in and readjusts. However, the process takes place visibly abruptly and therefore contains (spectral analysis) significantly higher frequencies. What remains is the practical maximum size of the diaphragm area and the required construction, to be determined by each individual. For these individual requirements loudspeakers have to be developed in corresponding, always limited sizes. And these should convert as correctly as possible within the physically possible transmission range. |
|
Control by analog sensor Similarly problematic is the correction of room induced cancellations. Regulation brings advantages at the lower transmission end, especially in the steady state. However, the steady state is completely subject to room resonance problems in the bass, with all the effects and limitations of attempting correction. Directly diaphragm controlled basses ignore changes in the radiation resistance of the room and therefore excite modes more than unregulated speakers or even microphonically controlled ones. This is because the controlled loudspeaker doesn't act as a "soft bass trap" but as a "hard wall" with regard to any external excitation of the diaphragm that doesn't succeed. However, the difference to unregulated loudspeakers is only slight, as there is an extreme acoustic mismatch. In the bass you would have to correct the room, otherwise it makes no sense. But this is only possible to a very limited extent, and if so - for which space in the room? In addition, room resonances easily cause 10 dB amplitude fluctuations. That's mighty compared to the effect of a control. So the detector must be at the listening position! In the middle and especially in the upper transmission range of a chassis the manifold resonance phenomena (membrane resonances, resonances of or with the spider and with the edge suspension etc.) can no longer be detected inductively. The resonances no longer have a clear effect on the drive system with their kinetic energy. A control is therefore no longer possible in a meaningful way in the largest part of the transmission range. A control system works better here. |
|
<zurück: Myroklopädie>
<zurück: Myro>